ABC448
またまたDまで4完。最高レート更新が続いている。パフォは過去10回のうち7回で緑パフォなので、上がり続けていると言うより、今年に入ってからパフォが上がり、レートが遅れて付いて上がってきている。
C問題まで22分というのは初めてかも知れない。想定解法とは違い、multisetで愚直にシミュレーションしてAC。
D問題は40分弱でACできた。1時間以内に4完すれば緑パフォは取れるようだ。setをdfsの引数に非ポインタ渡しにしていて、MLEかつTLEを食らった。setをdfs外に静的に確保し、dfsの頂点に入る時にinsertしたかを覚えておいて、insertした頂点から離脱するときにだけsetからeraseしたらうまくいった。
E・F問題はさっぱり分からず。FはHeuristic的な思考で解けたようだ。
ABC447
前回と同様、Dまで4完。最高レート更新が続いている。入緑まであと70、このペースで緑パフォを出し続けられれば、4月頃には入緑できる可能性あり。
C問題は書きながら想定解法に辿り着いたので、提出コードの長さの割には30分以上かかってしまった。
今回もD問題の方が早く20分弱でACできた。想定解法どおりで、コードも実質10行程度。
E問題はサンプルは通ったがTLE。Union-Findのグループ数を取得するために、uf.groups().size()としていたのが不味かったと後で知った。groups()はO(N)の計算量である。
AHC061
久しぶりの長期AHC。問題を読んで有効な作戦がピンと来なかった。外周部は狙われにくいなど囲碁っぽい感じがした。AIが得意そうな問題だったのと忙しかったのもあり、自分的にはやる気を出せず、10日間に1回も提出さずに終了。回答例もあったので、それをそのまま提出することも可能だったが、レートが下がりそうだったのでやめた。
ABC446
Dまで4完。最高レート更新。Cはqueueを使うのが普通のようだが、自分はqueueを使わず、仕入れた卵の数の配列Aを使用した数Bだけ減らし、冷蔵庫にある最も古い卵の仕入れ日を管理する方法でACした。まあ、queueというデータ構造も中身はvectorとtop位置のポインタの組み合わせだから、本質的には同じか。
D問題は意外と早く10分強でACできた。普通に想定解法に到達した。これはDPの一種とみなすこともできるようだが、自分はDPという認識は全く無かった。ただ、提出コードを見直すと、確かにDPと同じ構造をしている。
E問題は全く分からず、まだ40分程あったので、本番中としては初めてF問題にトライ。サンプルは通ったがTLEで爆死。まあそんな甘くないわな。
ARCのクラス分けが近日中に変更され、レート800から参加できるようになるらしい。つまり入緑すればrated参加できるので、なるべく早く入緑しておきたい。
ABC445
Cまで3完。Cは珍しい制約条件に最後まで気づかず、他の人も苦戦していたようである。Dは全く回答思いつかず。
ABC444
Dまで4完。最高レート更新で茶色瓦4枚(700以上)に到達。最近5回中4回緑パフォを出せており、入緑が見えてきた気がする。ここ1年毎週ABCに参加して解説放送を復習しただけで特に何か始めたわけではないが、D問題をACすることが当たり前とは言わないが普通になってきた。なぜだろう。
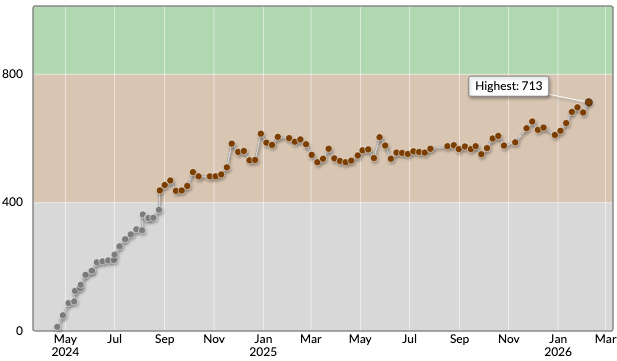
C問題は飛ばしてD問題を先に正答したが、E問題が残り時間で解ける気がしなかったし、C問題に設定されている以上、解けるはずと信じて考察を深めたところ、折れたじゃがりこに着目するとmaxとmin、max-1とmin+1、、、がそれぞれ対応することに気付けた。
A問題は111の剰余で判断という解法が秀逸。開始9秒でACした人がいるが、ゾロ目判定の問題を予測して回答を準備していたのだろう。
AHC060
最近、短期AHCで山登りにトライしようとして、スコアを返すシミュレーション関数を作るだけで時間が溶けてしまう失敗をしていたので、今回は従来通りまず回答を作成する関数を作成したら、出だしは良かった。その後シミュレーション関数を作ったが、今回は楽に作れた。手順は以下のとおり
・Tターンまで全ショップを適当に巡回し続け、100ターンくらいしたら、たまに苺に変えていく。
・全ての店で持っている文字列をsetに入れておいて、含まれていない文字列になった時点で、最寄りの店に直行する。ただし逆行禁止ルールがあるので、直行ルートが逆行する場合はアイスの収集を続けるようにした。
久しぶりの水色パフォ。
ABC443
Cまで3完。DとEもサンプルは通ったが、正解からは距離はある感じ。Dは上位からpriority_queに入れていく解法が自分がやろうとしていたものに近い。Eは正解は理解したが、自分では何度やっても正答しないので諦めた。
ABC442
今回もA-D4完で最高レート更新!最近、緑パフォを出すことが増えてきたので、入緑も見えてきた。
Dまで40分以内で簡単だなと思ったが、やはり皆解けていたようで、D問題なでも灰diff。初めてじっくりE問題に取り組むことが出来た。始めはatan2関数で偏角を求める解を提出したが1WA。整数だけの取り扱いにするため外積でやれば良いとは気づけなかったのは悔しい。外積なんて普段から使っているのに。
ABC441
A-D4完で最高レート更新!やった。C問題は考察メインの問題だが、自分でもよく思いついたと思う。E問題は、雰囲気的に尺取りかと思いましたが、範囲の増加に単調性がないため、尺取法は使えないらしい。
ABC440
Cまで55分かかったがACできた。Cが意外と正答率が低かったらしく、今回は緑パフォとなりスコアアップ。Dは解けたと思ったが、1ケースだけTLE。もう一段、2分探索にする必要があったようだが、時間切れ。
AHC059
短期AHCは4時間しかないが、正しくスコアを吐き出すシミュレーション関数を作るだけで半分以上の時間を要してしまう。戦略としては上位者の解説と同じく、操作3抜きで操作2を行う順列を作る問題と捉え、途中についでに拾えるように、vector<vector<int>>の形で手を表現した。それを最適化していくロジックを組んでいる間に時間切れ。
前回に引き続きレートを大きく割る結果になってしまったが、レート更新は±ゼロ。AHCの採点方式が変更されて以来、下がりにくくなったのは有り難い。
ABC439
Cまで30分で解けたので、辛うじてスコアアップ。DはTLE解までたどり着き、あとは2分探索化すればOKなところで上手く実装できず。
ABC438
C問題をDFSで解こうとしてハマる。stackを全く思いつかず。stackを使う問題(BFSを除く)はレアなので、忘れた頃にやってくる。2階連続でスコアダウン。
ABC437
都合が悪くunrated参加。CはDPかと思ったが、愚直でOKだったようだ。
ABC436
B問題に20分も掛けてしまった。負の数のmodを取るときの考慮漏れ。その代わりにC問題は8分でAC。
D問題は最後までMLEとTLEに悩まされた。入力例3のように全て同じワープ文字だった場合、計算量がO(H2W2)になることに気付けなければいけなかった。悔しい。
ABC435
C問題簡単だったはずなのに、DFS解法に走ってしまってTLE地獄から抜け出せず。30分くらい時間を溶かした後に、別方針で一から書き直してAC。すごく短いコードだった。D問題は時間切れになったが、終了後10分でACできたから、C問題の時間ロスが悔やまれる。
ABC434
Cまでしか解けなかったが、31分で解けたら、緑パフォにはなるんだな。
AHC057
かえでさんが凄い点を叩き出した。Heuristicは年齢も性別も関係ないと勇気づけられる。生成AIをうまく活用というのも、まるで若手のよう。
https://atcoder.jp/users/kaede2020?contestType=heuristic
ABC433
Dまで4完で久しぶりに緑パフォ行けるかも。
A問題でまさかのWAを食らったが、Cはすぐ解けた。
D問題はlong longでもオーバーフローする場合があるのに気をつける必要がある。
AHC056
・全マス別の色にする
・BFSで最短ルートを全目的地に対して求める。
・目的地を内部変数として色と最短ルートをルール化する
・全目的地を通して使っていない色は別の1色にする(Cの削減)
・状態を共有していない色どうしを統一色にする(Cの削減)
・一度も交差しないルート同士を同じ内部変数にする(Qの削減)
・邪魔石を置いて似通ったルートを統合する(Qの削減)
Qを削減するため、(色と状態)に対するA,S,Dの値が全て同じであれば更にQを共用できることに気づき、実装を試みたが最後まで正解を出せず、単に重複を避けた圧縮にとどまる。
Tに余裕があるので、似たような経路は多少遠回りしてでも共通化するのがポイントなんだろうけど、邪魔板を置いてみるくらいしかアルゴリズムが思いつかず。邪魔板の位置と方向で山登りすると、5個くらいQは減らせました。
↓ 0001の例とヒートマップ
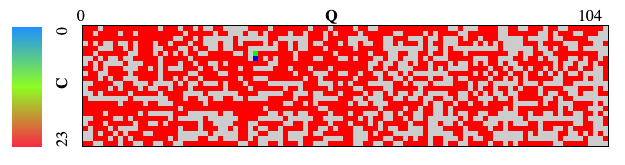
BFSではなくダイクストラを使っている人がいました。確かに、未使用のマスを通る場合はコストが高く付くように、重み付きグラフにしてやれば、経路の統合ができそう。
https://note.com/tetra4_cp/n/n6be697ae0f1d
ABC431
C問題まで19分で解けて行けると思ったら、それ以上解けず。
D問題はナップサック問題のDPなのはすぐ分かるが、DPが構成できず。。
ABC429_
C問題まで解けましたが、みんな解けていた灰diffレベルだった様で、また瓦2枚に下がってしまった。
D問題も解き方は分かったが時間切れ。
AHC055
思いつく実装は出来たが、なんか順位低い。山登りとか焼きなましには勝てないか。
ABC428
今日は何故か30分遅れて開始。Cまで解けましたが、endlの時間が長すぎてTLEで苦しみました。
デバッグ用にcerr << endl;が残っていただけでTLEだった。
ABC427
Bに手こずって時間取られてしまいましたが、Cは意外と早く解けた。Dは3分で諦めて、Eに1時間取り組んで終了。Cはbit全探索。
ABC426
Cは、Union-FIndを使って解けました。アップデートするOSをアップデート先のOSグループに融合していく感じ。このアルゴリズムを実戦で使えたのは確か2回目。
AHC054
最初の週末の時点で、AAを渦巻き配置のトレントで護衛する方針を立て、その時は100位以内。
一重の壁では、反対側のトレントが認知されていない時に、知らずに仲間で突き進んで偶然見つけられてしまう事があるので、2重の壁にしたらグンと上がった。
ただ、左上の(-2,-3)の位置にトレントを置くと、何故か1ケースだけWAになる不具合があり、最後まで解決できず。終了後の3000ケースのシステムテストでも引っかかる恐れあり。
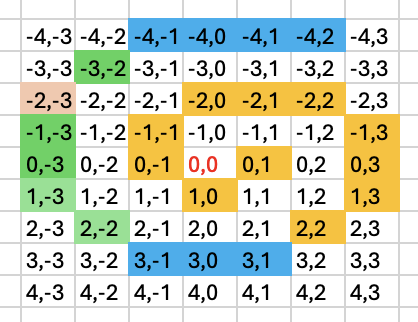
その位置が森の入口になるレアケースであることが判明。初手だから不要と思って入れていなかった確認済み判定を追加したところ、全てAC。
ABC425
Cは累積和とIMOS法でできるかと思いきやとなり出来ず。累積和だけO(N^2)のTLE解までは作れた(サンプルはACするが意味無し)。解説を見たが、これは全く思いつかず。
ABC424
CはDFSで解けましたが、バグ取りに30分以上かかった。
DはDPなのは分かったが、能力がないので諦めてw,
Eは長さと本数のペアを管理すれば解けそうだったが時間切れ。後で続きをやってみよう。
ABC423
Cのバグ取りが終わらず2完で終了。。
そして今CもAC。。。戦略はあっていたのに。
AHC053
今日ABCかと思って21時にスタンバったら19時からAHCだったorz
2時間でもやりたいことは出来たかな.というかそれくらいのアイデアしかないとも言える.
1.全部の山をLで埋める.
2.残りを見ながら,大きいカードから順に載せられるところが無くなるまで山に積んでいく.
なんと、前回のAHCの1位の人は、延長戦でさらに工夫して、全ケース満点を取れるプログラムが出来たそうです。しかも、山登り解法に近いものの、演繹的なアルゴリズムっぽい。
https://yosupo.hatenablog.com/entry/2025/09/15/213945
ABC422
Cまではミスりつつも順調。
Dは公式解説よりも、snukeさんの逆から解く方法が秀逸。
E問題も解けそうで解けず。乱択という戦法は思いつかなかったが、思いついても良さそうで悔しい。
ABC421
点数が高いのでやる前から難しいのは分かっていたが、、ここまでとは。
ABC420
D問題、2枚のBFSという戦略自体は合っているようだが、実装がうまく行かない、、、
とおもったらif文のバグだった。
ABC419
D問題まで解けた!いわゆるimos法ですね。
E問題を悩む残り時間もあったが、貪欲法ではなかったようだ。
AHC051
交差しない有効な木構造を構築するアルゴリズムが思いつかず.
score関数だけは作れたのですが,結局提出0で終了
ABC417
時間が合わず参加できませんでしたが、後から解きました。Cまでは解けました。Dは単にDP組んでも駄目なようで無理。
ABC416
D問題。multisetの二分探索をするとき、multiset::lower_bound()を呼べばO(log(N))だが、std::lower_bound()を呼ぶとO(N)になってしまう罠。multisetのインスタンスからメソッドを呼ぶ必要がある。
ABC415
最近、C問題のレベルが高い。
ABC414
C問題。解けそうだったが時間切れ。終了直後にAC。一部reverseしてなかっただけだったorz
ABC413
D問題、サンプル3つは通ったが、やっぱりだめだった。
絶対値でソートしたものが等比数列であることは必要条件で、あとは、交互にプラスマイナス、もしくは全部プラス、もしくは全部マイナスならOKかと思ったが違うみたい
そうか、絶対値にしてソートではなくて、絶対値を基準に(値は絶対値を取らずに)ソートすれば良いのか、、、
https://atcoder.jp/contests/abc413/submissions/67363952
↑のもう一つのテクニックとして、以下のif文。
if (a[i]*a[i+2] != a[i+1]*a[i+1]) ok = false;
少数になるリスクが有る割り算を避けて、整数の掛け算だけで等比数列を判定する方法。
ABC411
Dが逆から解けるのが未だに理解できない。
ABC410
Dは5WAが消せず諦め。Eも解けたと思ったがTLE。悔しさなし。
ABC409
B問題に手こずる。setはランダムアクセスイテレータでないため、イテレータfor文で回す必要があることを学んだ。
AHC048
余り何色も混ぜようとするとパレット構造が複雑化しそうなので、ターゲットの色を最も良く表現できる三原色を選び出す、というアプローチで解きました。
解法1
・色をCMY3次元空間のベクトルとみなす。
・ターゲット色を任意に選んだ3色の絵の具ベクトルに成分分解。
ここでは、逆基底を求める方法を用いた。
ターゲット色(c, m, y) = a*絵の具1(c, m, y) + b*絵の具2(c, m, y) + c*絵の具3(c, m, y)
・この分解を持ち絵の具の組み合わせで全探索し、最も良い組み合わせを三原色とする。
・色を抜く操作は出来ないので、このa, b, cが全て正でなければならないが、ここでは、min(a,b,c)が最大となるものを三原色とした。
・選んだ三原色をa,b,cの配合で混ぜるようにウェルを色々組み替える。
この解法は精度が高いですが、ウェルの組み換えに手数を多く消費するので、Tが10000以下のケースでは対応不能。
解法2
・解法1は手数を消費し過ぎなので、もっと手数の少ないアルゴリズムを考えた。
・a,b,cを演繹的に求めるのではなく、a,b,cは0か1しか取らないとして、これもbit全探索して、最良同士を更に比較して三原色を選定。
・一度作ったウェルに残った絵の具もリスト化しておいて、ある程度近い色が残っていたら、新たに作らずそちらを提出。
・0か1なので、ウェルの組み換えは不要となり、1000色で最大でも2000ターン程度で完了。
実際は最大ターン数を見て解法1と2を切り替え。
中には、解法2の方がスコアが良いケースもあるので、その場合は解法2を提出。
ABC408
Cの解法に気づくのに時間がかかってしまった。Dは解ける気がせず。
ABC407
自分的にはまずまずの出来かな。dfsに慣れてきた感じ。
ABC406
なにこれ、、爆死。
ABC405
D問題で初めて多始点BFSを使って残り10秒でAC出来た。嬉しい。
しかし、B問題でハマって順位はそこそこ。
ABC404
D問題、3^10回全探索できるのは気付いたが、3^nの全探索の手法が分からず。A問題は、いかに速く解くかですが、この解き方が良いと思いました。
REP(i,N) vis[S[i]-‘a’]=1;
文字ごとの出現の有無をこの一行で集計。
AHC046
ブロックを設置しない愚直解から先に一歩も進めず。同じような人が435位に群がっている。。。
ABC402
D問題。平行なペアの組み合わせを除くのは分かったが、幾何学的に三角関数使いまくったら何故か22WA