先日の長征5Bに関する記事で、SLS Block Iの1段ロケットは高度40km×1806kmの長楕円軌道に投入されることを述べた。近地点が大気圏内にめり込んでいるため、分離された1段ロケットは1周地球を回ってきた後に大気圏に突入する。その時間と場所を特定し、予告できるため、安全な投棄方法である。
オーベルト効果
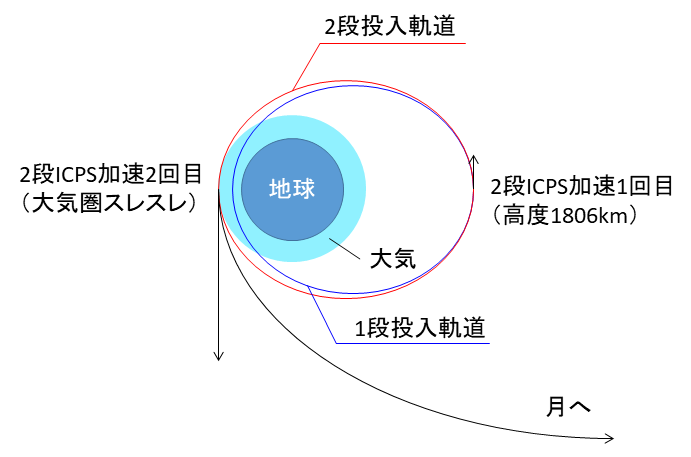
SLSの1段目が投入する軌道の遠地点(高度1806km)に到達すると、SLSの2段であるICPSを点火して僅かに加速し、近地点高度が40kmから100kmまで上げられる[1]。この下図の赤線の楕円軌道を周回しているとき、もう一度エンジンを点火して地球を脱出し、月へ向かいたいが、最も効果的な加速位置はどこか。
地球の重力圏から脱出するためには、地球の重力ポテンシャルよりも大きな運動エネルギーを与える必要がある。同じ\(ΔV\)の加速を行うなら、運動エネルギーの増加は常に同じか?そうではない。初期速度\(V_i\)が大きいほど、加速による運動エネルギーの増加は大きい、というのがオーベルト効果である。もちろんあのヘルマン・オーベルトである。質量\(m\)の変化が無視できるとすると、運動エネルギーの変化は、
$$\frac{1}{2}m(V_i+\Delta V)^2 – \frac{1}{2}mV_i^2 = mV_i\Delta V + \frac{1}{2}m\Delta V^2$$
確かに、右辺第1項は加速前の速度\(V_i\)に比例して増加する。よって、先ほどの問いの答えは、最も速度が高くなる近地点が最適ということになる。
更に、近地点通過時の速度は、近地点高度が低いほど速い(ケプラーの第二法則)。よって、SLSが近地点高度を100kmを狙う理由は、空気抵抗による減速は避けつつも、大気圏スレスレの高度を狙って近地点速度を上げ、オーベルト効果を最大限利用して地球の重力ポテンシャルエネルギーから脱出するためである。100km以上の近地点高度としてしまうと、\(V_i\)が減って損をする。
2段ロケットの捨て方
この後の上段ロケットが月へ向かう軌道に遷移する過程を調べると、再びオーベルト効果を使って効率的に加速し、その加速に用いた2段ロケットはその後、月フライバイで加速して太陽周回軌道に投棄される、すなわち惑星にして捨てるという、巧みな事をしているようである。これについてはまた別の記事にしようと思う。
参考文献